Design and Implementation of a Parallel Relational Database from scratch

[Report] [Presentation] [Code]

Summary

The project is an effort to design and implement a Relational Database from scratch and a subset of its many operations while incorporating the various concepts gleaned from the Programming Parallel Algorithms Course and related ideas inherent to the domain of Parallel Computing. This project was developed and implemented as part of the Programming Parallel Algorithms Course during my Graduate Study.

Abstract

The exponential growth of data, driven by innovations like the internet, smartphones, and personal computers, to name a few, has made databases a cornerstone of modern software applications. As data scales up, storing, managing and querying this data efficiently has become increasingly complex. In this regard, databases serve as the backbone to store, manage, and retrieve vast amounts of structured information in an organized manner. However, designing large-scale, efficient databases presents many challenges in terms of both design and performance. With the diminishing returns of Moore’s Law — which historically predicted continuous improvements in processor speed and computing power through more transistors — there has been a significant shift towards leveraging Parallel Computing. This shift has become increasingly pronounced with the rise of multicore and multiprocessor systems, which have become ubiquitous in modern hardware. Thus, parallelism offers a potential solution for improving database performance by utilizing the power of multiple cores and processors. This project is precisely such an effort to design and implement a Parallel Relational Database.

Implementation Details

The results of the project along with the related implementation details are summarized as follows:

• A parallel relational database supporting a subset of the typical CRUD (Create, Read, Update, Delete) operations has been designed and implemented.

• Various CRUD queries fundamental to the functionality of a Database have been implemented as below:
  • Creating a Table
  • Setting a Primary Key
  • Inserting rows into the table
  • Enforcing the Primary Key Constraint
  • Updating the rows of the table including conditional updation
  • Deleting the rows of the table including conditional deletion
  • Different variants of the Select Query including Selecting all the columns of all the rows, Selecting all the columns of rows meeting a condition, Selecting a subset of the columns of all rows, Selecting a subset of the columns of rows meeting a condition.

• Various aspects related to Parallelism have been identified and implemented as follows:

  • Select Search Query based on equality of primary key field: Here, a B-Tree has been implemented for indexing the table based on the primary key field. It was observed that the Select Search Query using the B-Tree implementation performed approximately 20x faster than the corresponding sequential implementation.

  • Select Range Query based on primary key field: Here, a B-Tree has been implemented for indexing the table based on the primary key field. It was observed that the Select Range Query using the B-Tree implementation performed approximately 2x faster than the corresponding sequential implementation.

  • Select all Columns for rows meeting a condition: A parallel for loop was used to implement this query. It was observed that the speedup was suboptimal (below 1) in this case with the speedup further decreasing with the increase in the number of threads. The main reason is that as this query requires displaying of the rows, the implementation uses a lock-based data structure to serialize the prints. As these overheads due to lock-contention are significant, there are no benefits due to parallelism for this query and it in fact worsens the performance as compared to the sequential version.

  • Select a subset of the Columns for rows meeting a condition: A parallel for loop was used to implement this query. It was observed that the speedup was suboptimal (below 1) in this case with the speedup further decreasing with the increase in the number of threads. The main reason is that as this query requires displaying of the rows, the implementation uses a lock-based data structure to serialize the prints. As these overheads due to lock-contention are significant, there are no benefits due to parallelism for this query and it in fact worsens the performance as compared to the sequential version.

  • Order by Ascending Query: A Parallel merge sort was used to implement this query. It was observed that the Parallel version achieved a maximum speedup of 2.2 for 16 threads, thereby denoting that there were some benefits due to parallelism.

  • Order by Descending Query: A Parallel merge sort was used to implement this query. It was observed that the Parallel version achieved a maximum speedup of 1.36 for 8 threads, thereby denoting that there were some benefits due to parallelism.

  • Group by Count Query: Here, two different parallel versions were implemented:

    • Parallel Version 1: This initially performs a parallel merge sort followed by sequential traversal of the sorted rows to aggregate the count of the groups. This version achieves a maximum speedup of 6 using 32 threads as compared to the sequential version.

    • Parallel Version 2: This initially performs a parallel merge sort followed by a parallel algorithm to aggregate the count of the groups using parallel primitives like tabulate and filter. This version achieves a maximum speedup of 5.5 using 32 threads as compared to the sequential version.

    The Parallel Version 1 performs slightly better than the Parallel Version 2. This could be because the overheads introduced by version 2’s algorithm which requires the creation of additional data structures using tabulate and filter is quite considerable that it is outweighing any benefits due to parallelism.

  • Group by Min Query: Here, two different parallel versions were implemented:

    • Parallel Version 1: This initially performs a parallel merge sort followed by sequential traversal of the sorted rows to aggregate the min of the groups. This version achieves a maximum speedup of 5.3 using 32 threads as compared to the sequential version.

    • Parallel Version 2: This initially performs a parallel merge sort followed by a parallel algorithm to aggregate the min of the groups using parallel primitives like tabulate, filter and reduce. This version achieves a maximum speedup of 6.5 using 32 threads as compared to the sequential version.

    The Parallel Version 2 performs better than the Parallel Version 1. This could be because the parallel version 2 algorithm using primitives like tabulate, filter and reduce inherently contains more scope for parallelism as compared to parallel version 1 which is essentially sequential after the initial parallel sort.

  • Group by Max Query: Here, two different parallel versions were implemented:

    • Parallel Version 1: This initially performs a parallel merge sort followed by sequential traversal of the sorted rows to aggregate the max of the groups. This version achieves a maximum speedup of 5.7 using 32 threads as compared to the sequential version.

    • Parallel Version 2: This initially performs a parallel merge sort followed by a parallel algorithm to aggregate the max of the groups using parallel primitives like tabulate, filter and reduce. This version achieves a maximum speedup of 8.1 using 32 threads as compared to the sequential version.

    The Parallel Version 2 performs better than the Parallel Version 1. This could be because the parallel version 2 algorithm using primitives like tabulate, filter and reduce inherently contains more scope for parallelism as compared to parallel version 1 which is essentially sequential after the initial parallel sort.

  • Group by Sum Query: Here, two different parallel versions were implemented:

    • Parallel Version 1: This initially performs a parallel merge sort followed by sequential traversal of the sorted rows to aggregate the sum of the groups. This version achieves a maximum speedup of 6 using 32 threads as compared to the sequential version.

    • Parallel Version 2: This initially performs a parallel merge sort followed by a parallel algorithm to aggregate the sum of the groups using parallel primitives like tabulate, filter and reduce. This version achieves a maximum speedup of 8.1 using 32 threads as compared to the sequential version.

    The Parallel Version 2 performs better than the Parallel Version 1. This could be because the parallel version 2 algorithm using primitives like tabulate, filter and reduce inherently contains more scope for parallelism as compared to parallel version 1 which is essentially sequential after the initial parallel sort.

  • Group by Average Query: Here, two different parallel versions were implemented:

    • Parallel Version 1: This initially performs a parallel merge sort followed by sequential traversal of the sorted rows to aggregate the average of the groups. This version achieves a maximum speedup of 5.5 using 32 threads as compared to the sequential version.

    • Parallel Version 2: This initially performs a parallel merge sort followed by a parallel algorithm to aggregate the average of the groups using parallel primitives like tabulate, filter and reduce. This version achieves a maximum speedup of 8.3 using 32 threads as compared to the sequential version.

    The Parallel Version 2 performs better than the Parallel Version 1. This could be because the parallel version 2 algorithm using primitives like tabulate, filter and reduce inherently contains more scope for parallelism as compared to parallel version 1 which is essentially sequential after the initial parallel sort.

Results

• All the results are generated for a Person relation of 10000 rows containing id, first name, last name, age, country, salary as its fields

• Select Search Query based on equality of primary key field: The below graph summarizes the performance comparison between SELECT_PK_EQ_SEQ and SELECT_PK_EQ for a query to retrieve the rows of the Person relation (of 10000 rows) with id == 7312:
  
  
  

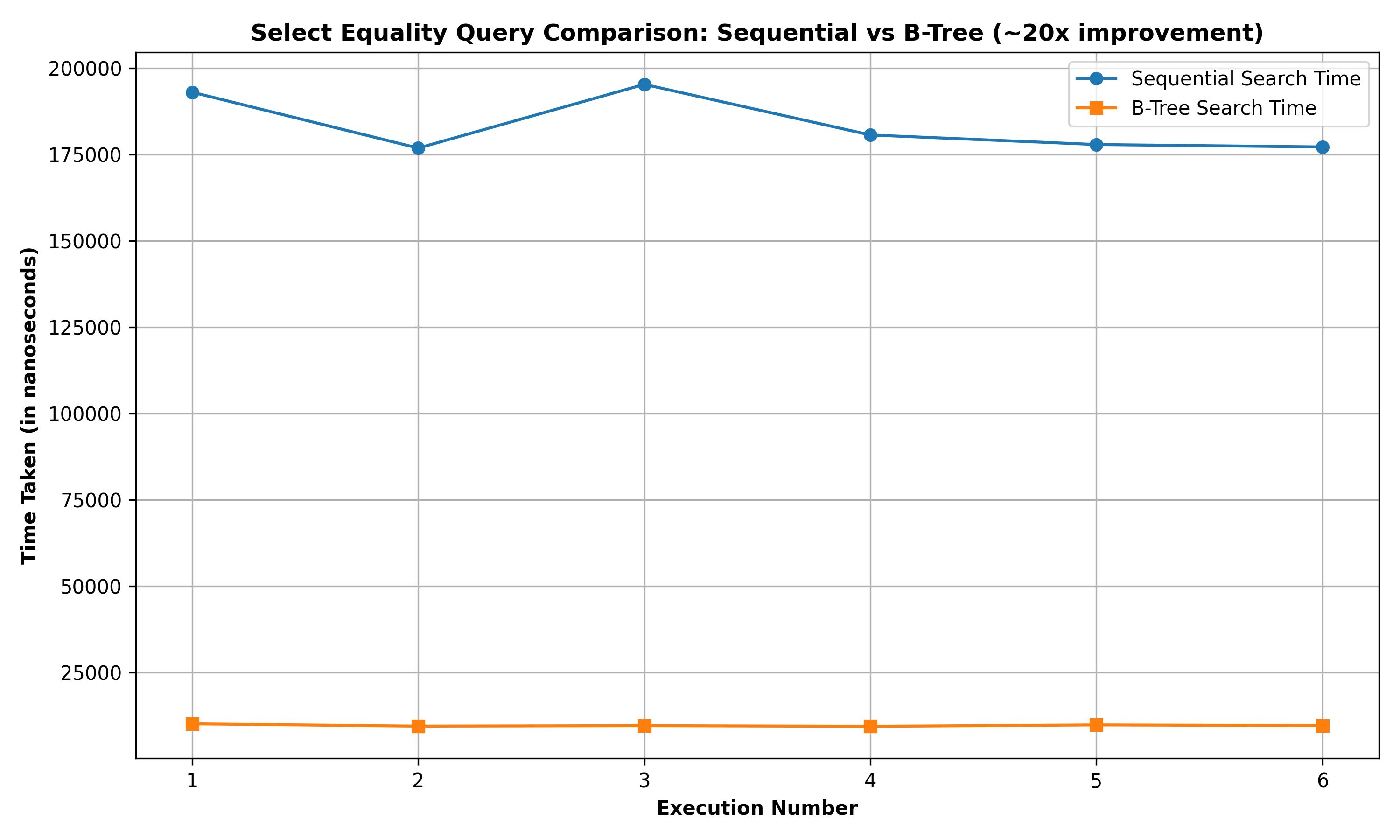
  It can be observed that the B-Tree implementation performs approximately 20x faster than the corresponding sequential implementation.

• Select Range Query based on primary key field: The below graph summarizes the performance comparison between SELECT_ALL_RANGE and SELECT_PK_RANGE for a query to retrieve the rows of the Person relation (of 10000 rows) with id >= 1291 and id <= 1524:
  
  
  

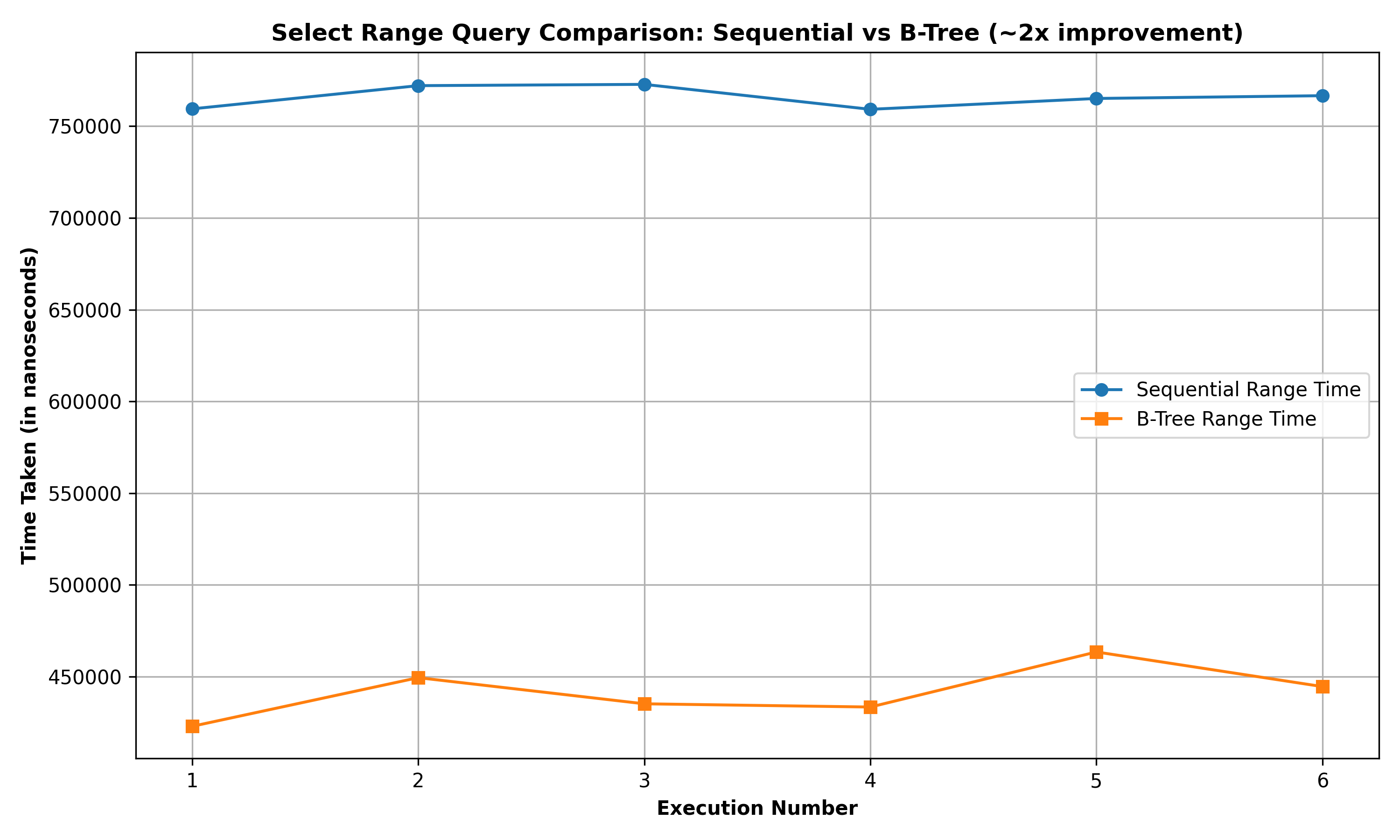
  It can be observed that the Select Range Query using the B-Tree implementation performs approximately 2x faster than the corresponding sequential implementation.

• Select all Columns for rows meeting a condition: The below graph summarizes the performance comparison between SELECT_ALL_COND and SELECT_ALL_COND_PAR for a query to retrieve the rows of the Person relation (of 10000 rows) with salary >= 250:
  
  
  

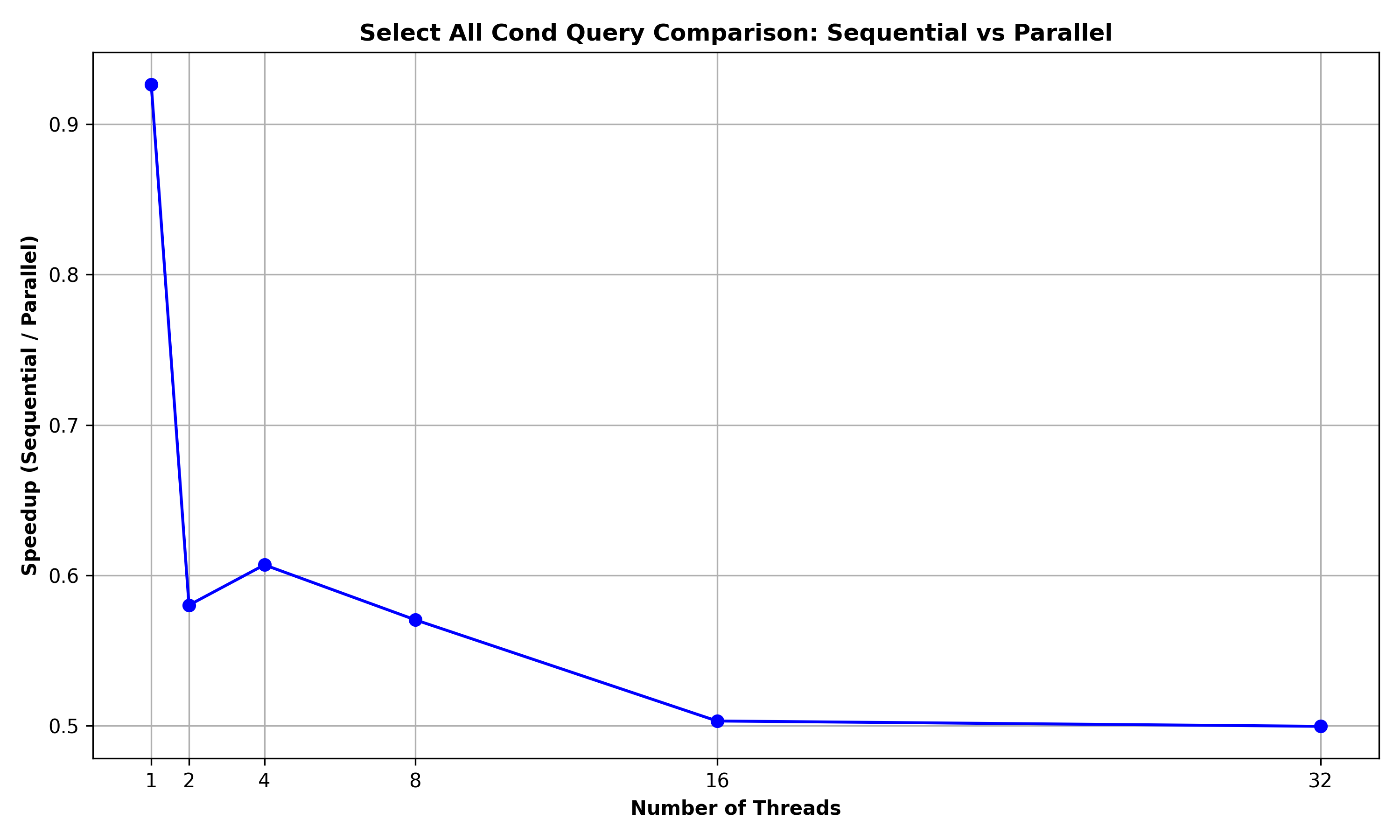
  Here, the speedup is suboptimal (below 1) and the speedup decreases with the increase in the number of threads. The main reason is that as this query requires displaying of the rows, the implementation uses a lock-based data structure to serialize the prints. As these overheads due to lock-contention are significant, there are no benefits due to parallelism for this query.

• Select a subset of the Columns for rows meeting a condition: The below graph summarizes the performance comparison between SELECT_COLS_COND and SELECT_COLS_COND_PAR for a query to retrieve the id, fname, age fields of the rows of the Person relation (of 10000 rows) with age >= 45:
  
  
  

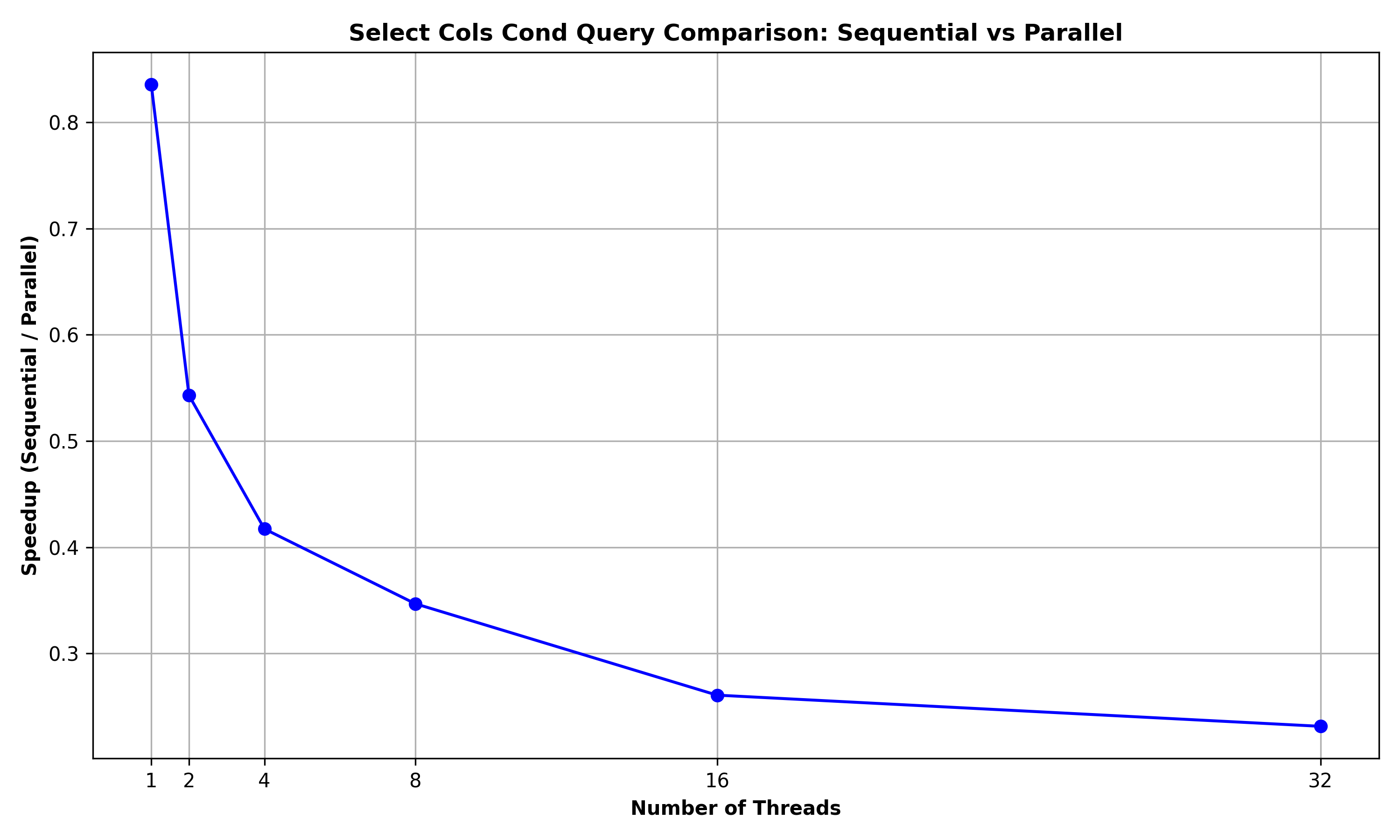
  Here, the speedup is suboptimal (below 1) and the speedup decreases with the increase in the number of threads. The main reason is that as this query requires displaying of the rows, the implementation uses a lock-based data structure to serialize the prints. As these overheads due to lock-contention are significant, there are no benefits due to parallelism for this query.

• Order by Ascending Query: The below graph summarizes the performance comparison between ORDER_BY_ASC and ORDER_BY_ASC_PAR for a query to order the rows of the Person relation (of 10000 rows) based on (fname, lname, id) fields:
  
  
  

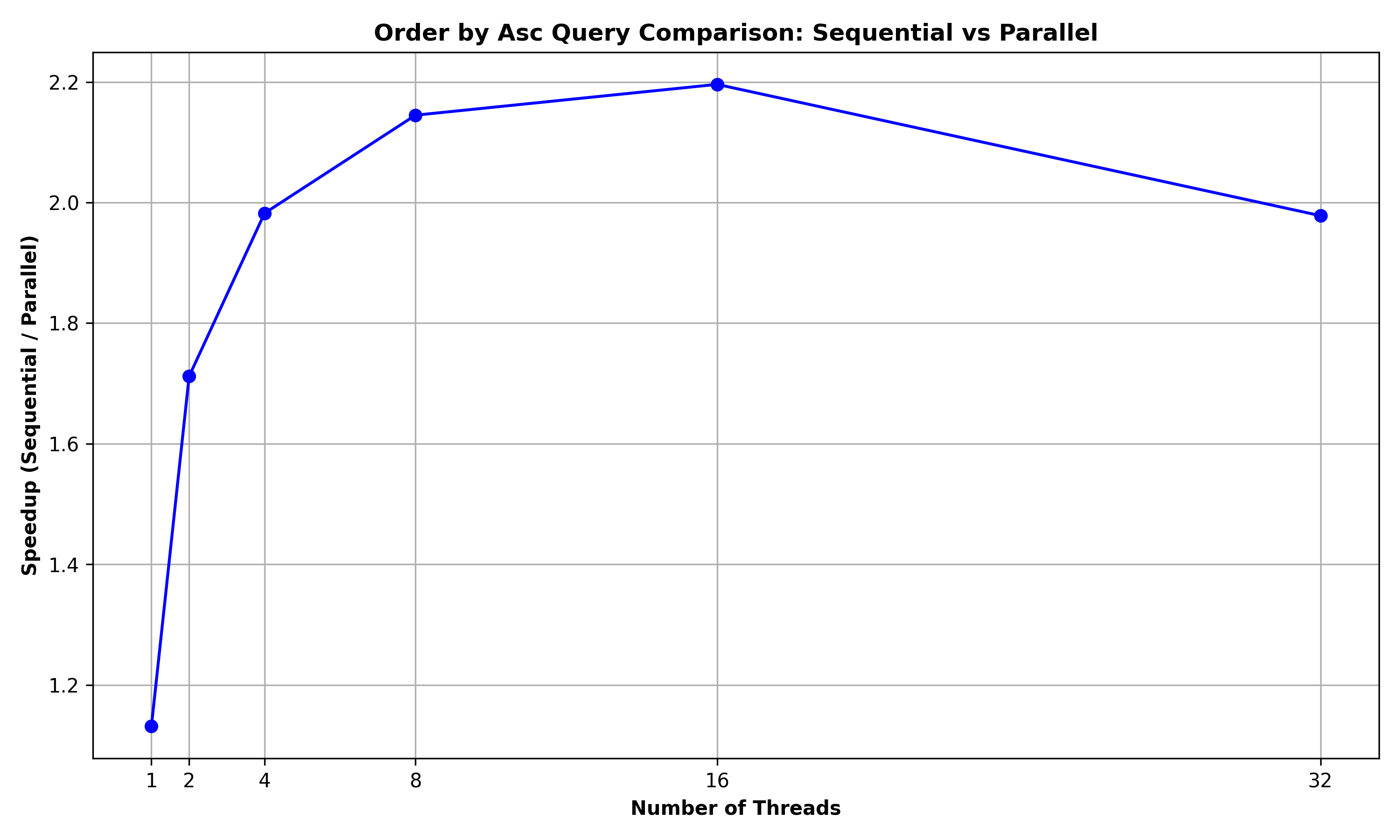
  It can be observed that the Parallel version achieved a maximum speedup of 2.2 for 16 threads, thereby denoting that there were some benefits due to parallelism.

• Order by Descending Query: The below graph summarizes the performance comparison between ORDER_BY_ DESC and ORDER_BY_ DESC _PAR for a query to order the rows of the Person relation (of 10000 rows) based on (salary, id) fields:
  
  
  

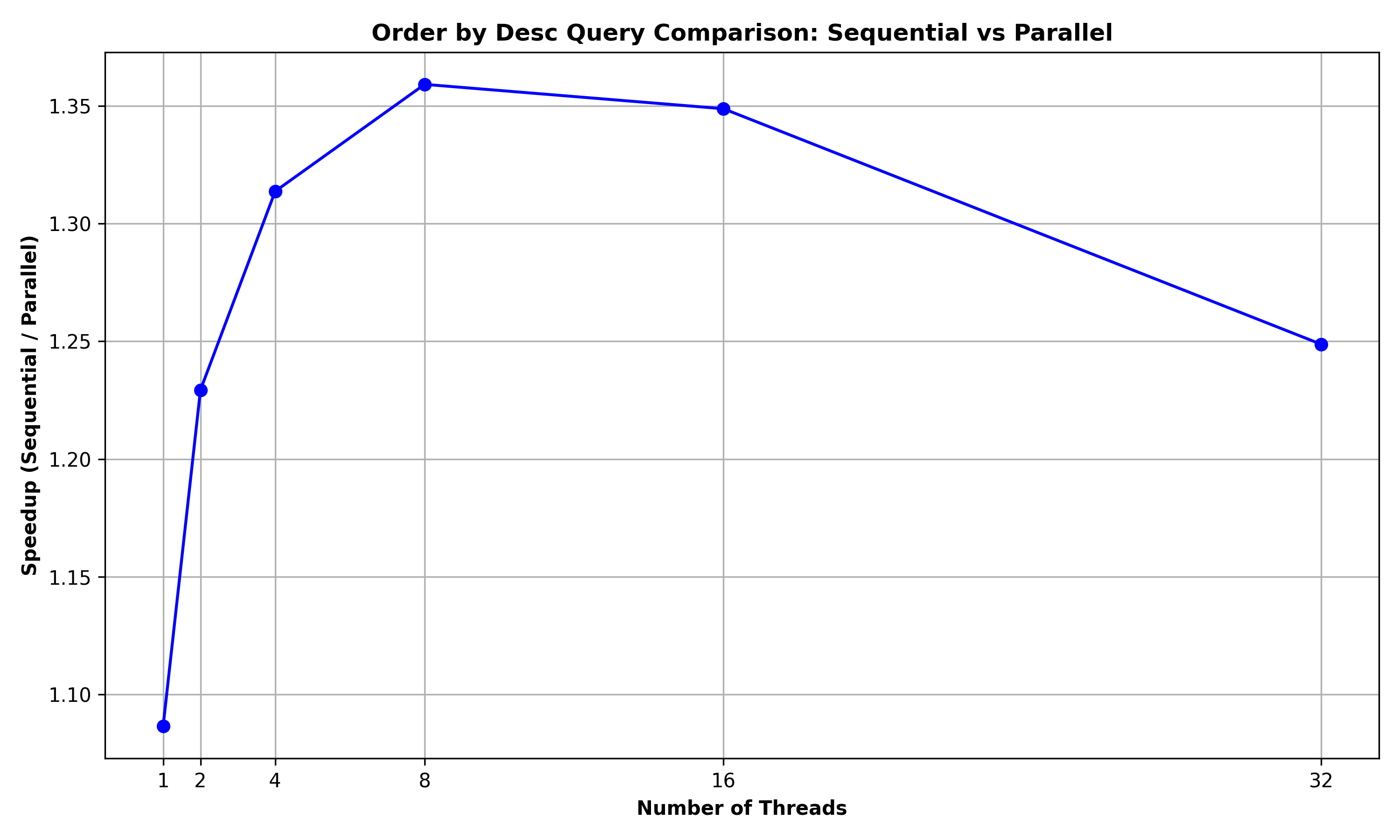
  It can be observed that the Parallel version achieved a maximum speedup of 1.36 for 8 threads, thereby denoting that there were some benefits due to parallelism.

• Group by Count Query: The below graph summarizes the performance comparison between GROUP_BY_COUNT, GROUP_BY_COUNT_PAR, and GROUP_BY_COUNT_PAR2 for a query to group the rows of the Person relation (of 10000 rows) based on (lname) and retrieve their counts:
  
  
  

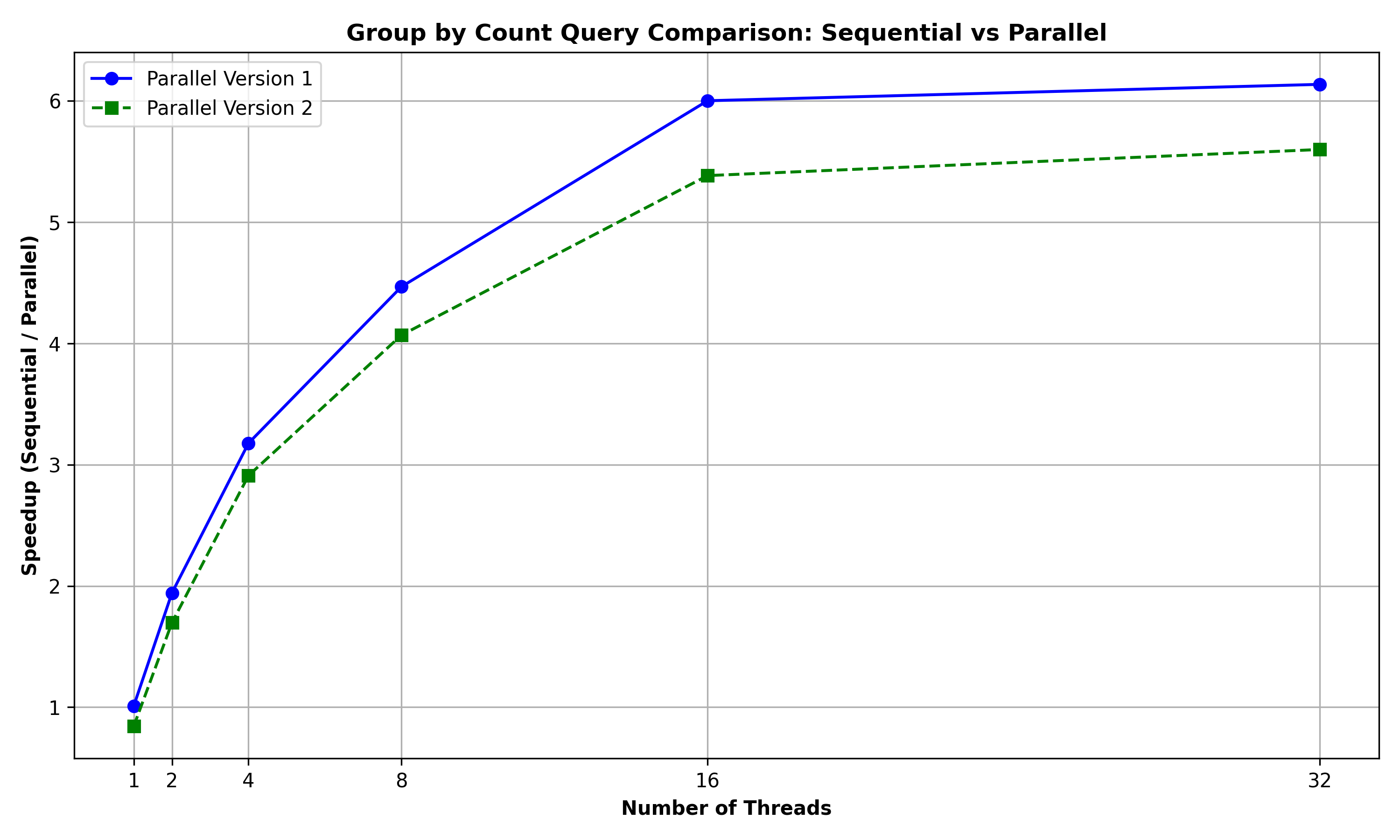
  It can be observed that the Parallel Version 1 performs slightly better than the Parallel Version 2. This could be because the overheads introduced by version 2’s algorithm which requires the creation of additional data structures using tabulate and filter is quite considerable that it is outweighing any benefits.

• Group by Min Query: The below graph summarizes the performance comparison between GROUP_BY_MIN, GROUP_BY_MIN_PAR2, and GROUP_BY_MIN_PAR2 for a query to group the rows of the Person relation (of 10000 rows) based on (country) and retrieve the minimum salary for these groups:
  
  
  

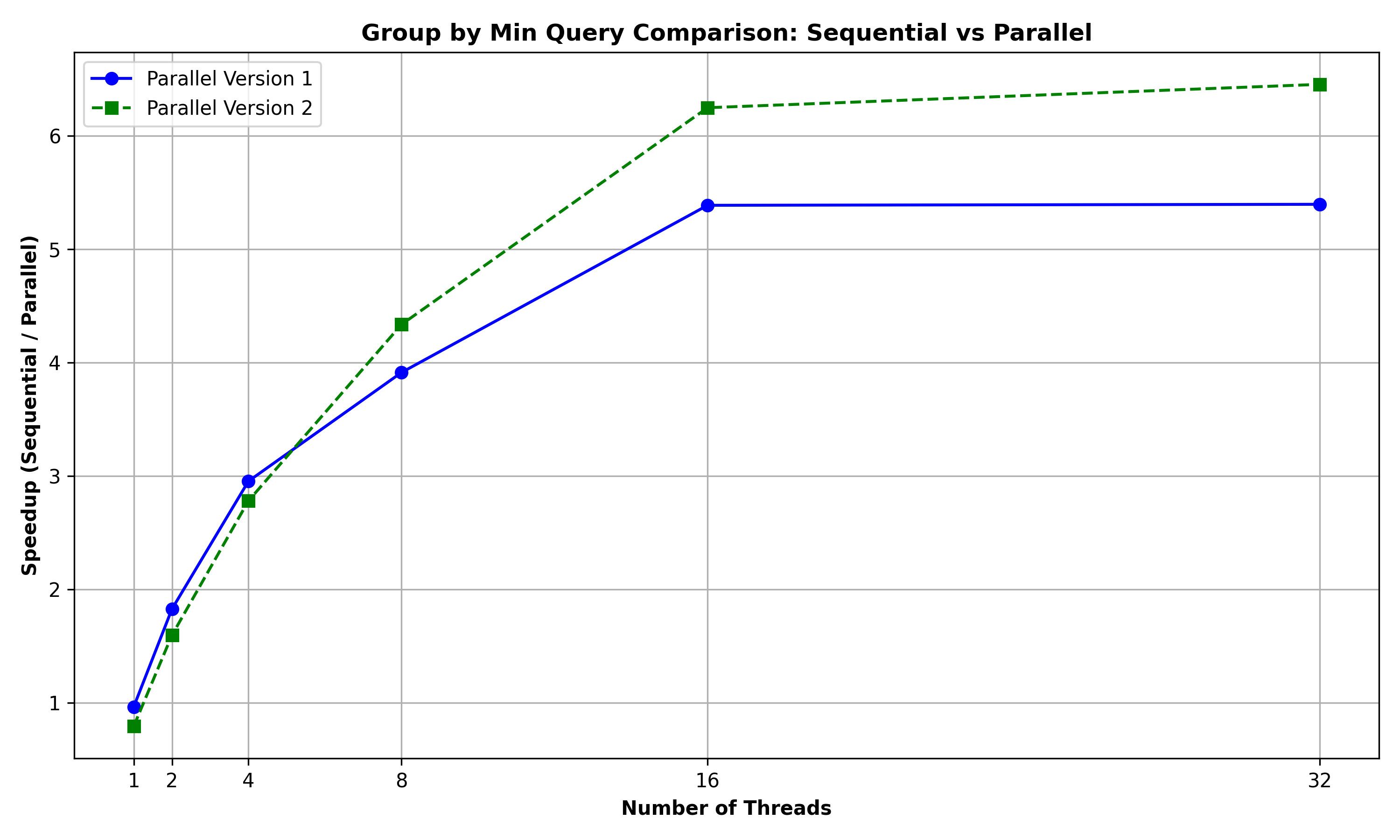
  It can observed that the Parallel Version 2 performs better than the Parallel Version 1 with the increase in number of threads. This could be because the parallel version 2 algorithm using primitives like tabulate, filter and reduce inherently contains more scope for parallelism as compared to parallel version 1 which is essentially sequential after the initial parallel sort.

• Group by Max Query: The below graph summarizes the performance comparison between GROUP_BY_MAX, GROUP_BY_MAX_PAR, and GROUP_BY_MAX_PAR2 for a query to group the rows of the Person relation (of 10000 rows) based on (country) and retrieve the maximum age for these groups:
  
  
  

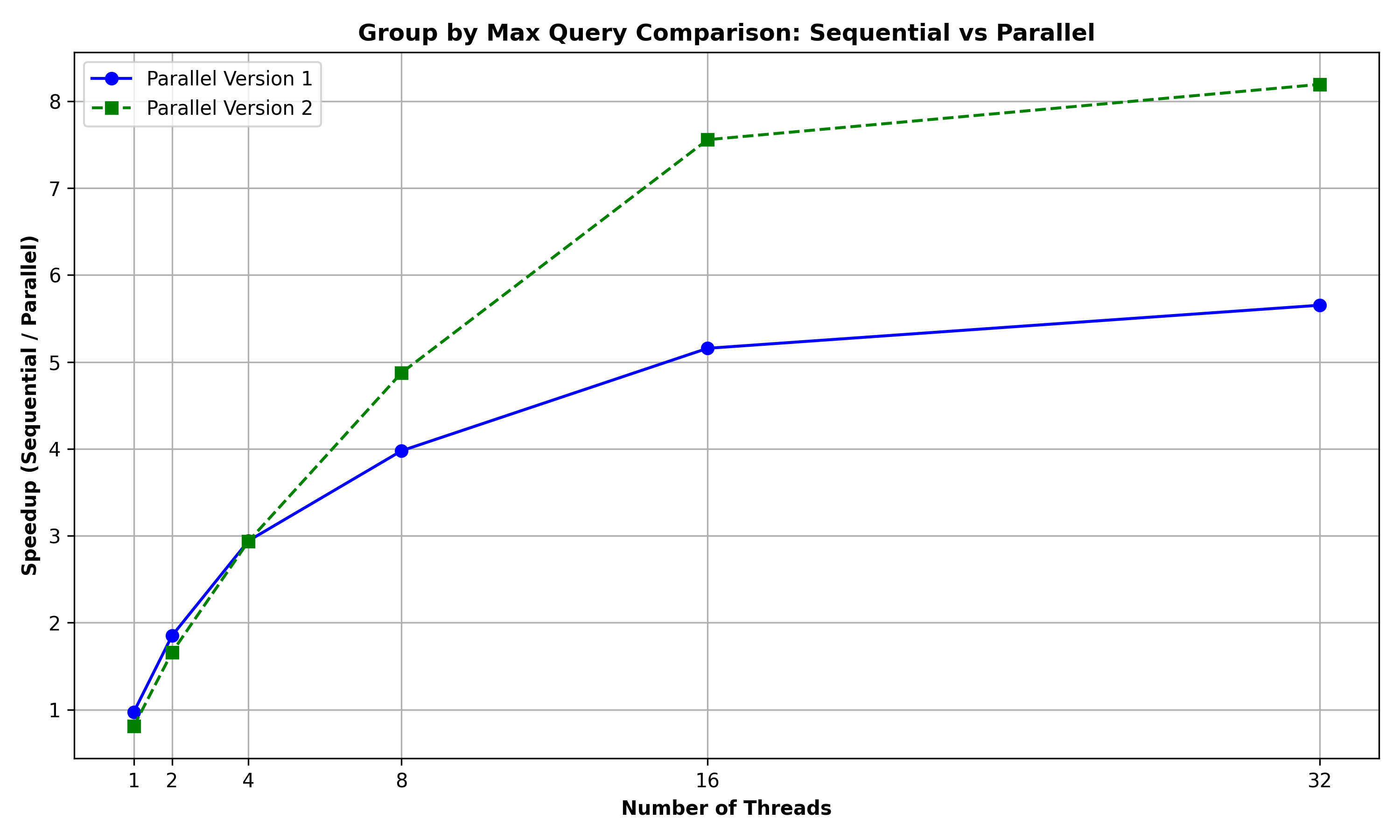
  It can be observed that the Parallel Version 2 performs better than the Parallel Version 1 with the increase in number of threads. This could be because the parallel version 2 algorithm using primitives like tabulate, filter and reduce inherently contains more scope for parallelism as compared to parallel version 1 which is essentially sequential after the initial parallel sort.

• Group by Sum Query: The below graph summarizes the performance comparison between GROUP_BY_SUM , GROUP_BY_SUM_PAR, and GROUP_BY_SUM_PAR2 for a query to group the rows of the Person relation (of 10000 rows) based on (country) and retrieve the sum of the salary for these groups:
  
  
  

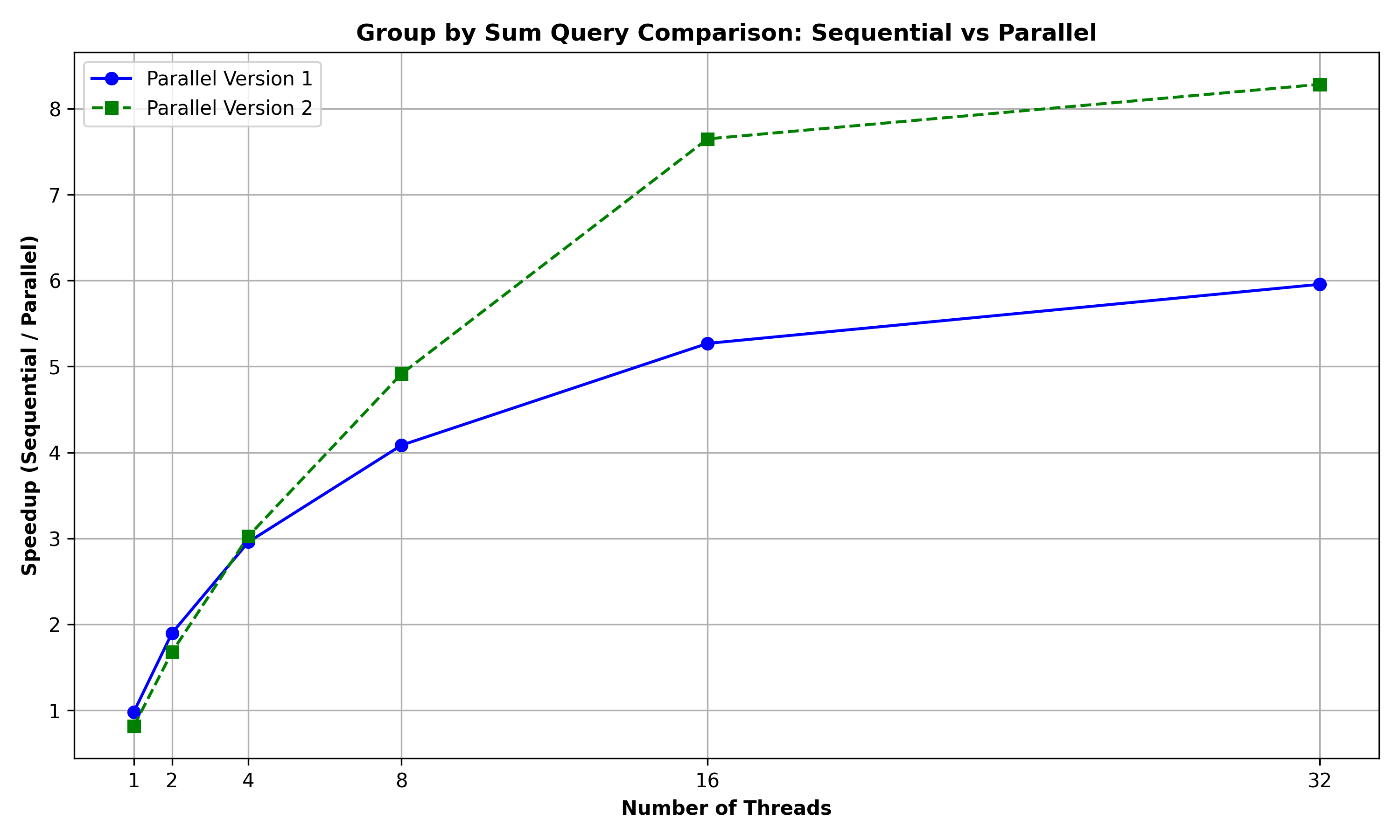
  It can be observed that the Parallel Version 2 performs better than the Parallel Version 1 with the increase in number of threads. This could be because the parallel version 2 algorithm using primitives like tabulate, filter and reduce inherently contains more scope for parallelism as compared to parallel version 1 which is essentially sequential after the initial parallel sort.

• Group by Average Query: The below graph summarizes the performance comparison between GROUP_BY_AVG, GROUP_BY_AVG_PAR, and GROUP_BY_AVG_PAR2 for a query to group the rows of the Person relation (of 10000 rows) based on (country) and retrieve the average of the salary for these groups:
  
  
  

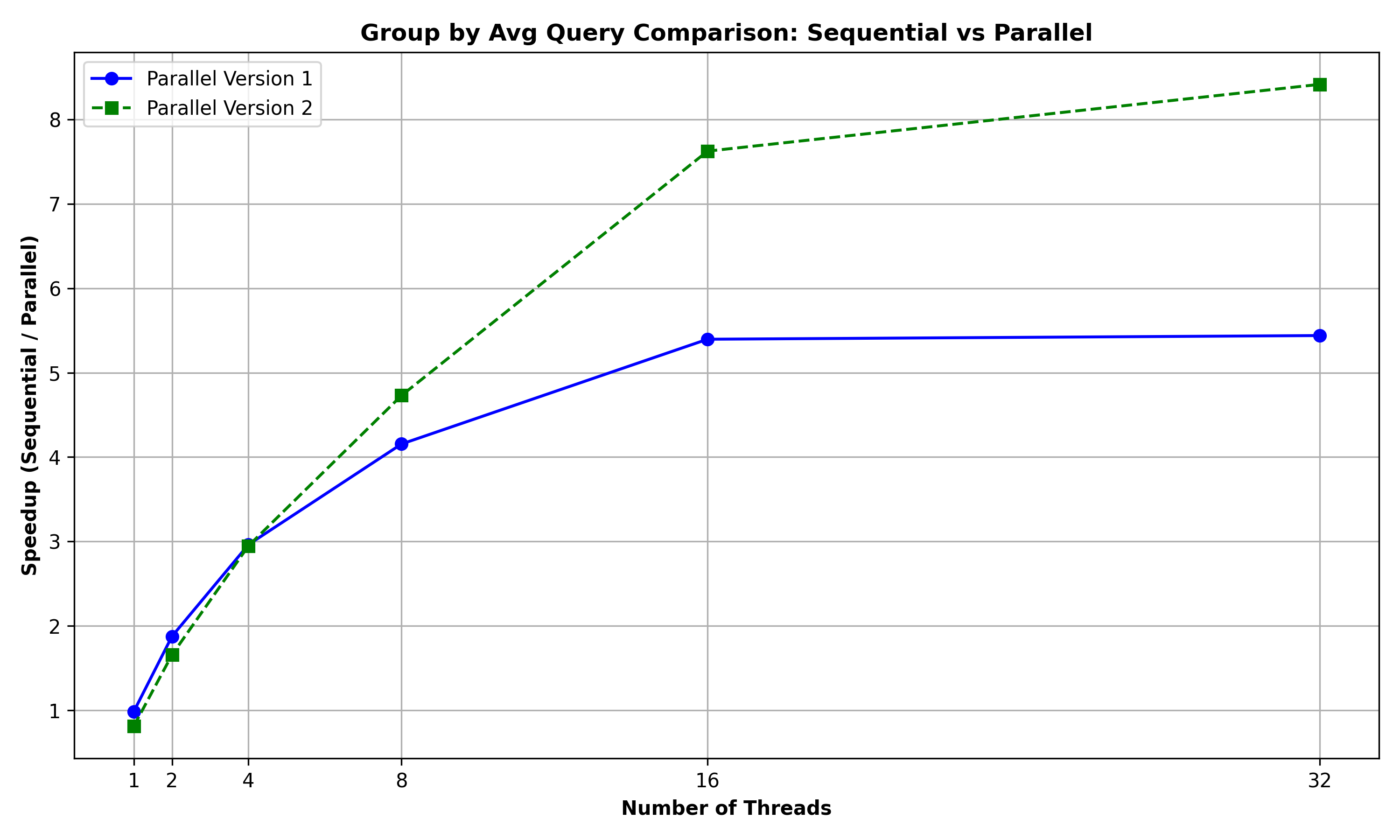
  It can be observed that the Parallel Version 2 performs better than the Parallel Version 1 with the increase in number of threads. This could be because the parallel version 2 algorithm using primitives like tabulate, filter and reduce inherently contains more scope for parallelism as compared to parallel version 1 which is essentially sequential after the initial parallel sort.